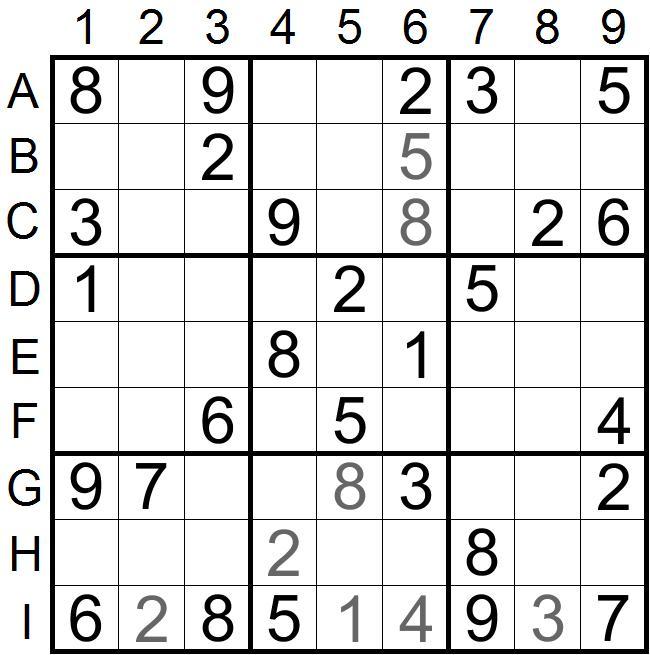
不知道大家是否从上图中找到了数对占位的位置，此示例其实找到数对占位难度并不大，这个位置还是比较容易发现的，也就是观察一宫、二宫和九宫的数字8、9在三宫内排除形成一个数对占位，来看下图：

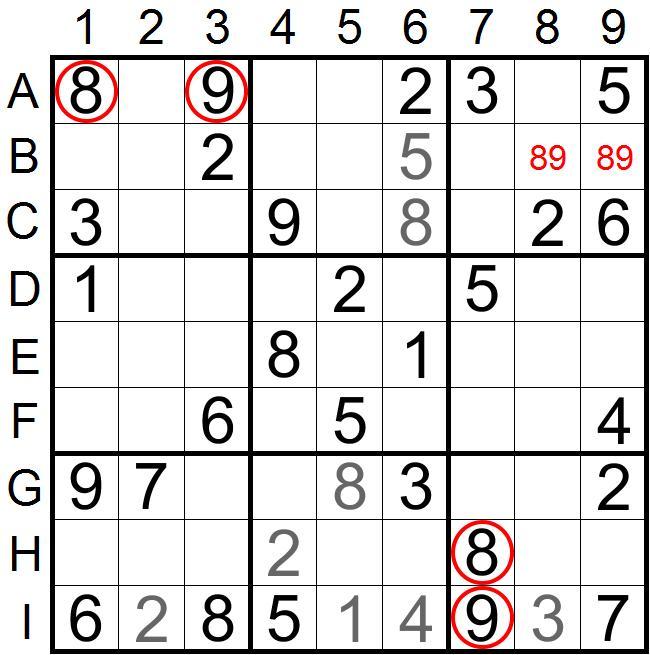
经过精简，二宫的8、9条件不使用，也可以根据一宫和九宫的线索得到三宫内数对8、9的占位。找到占位后，下一步如何出数呢？来观察三宫，剩余三个空格缺少数字1、4、7，周围都没有线索，无法在三宫出数，难道我们找到这个数对占位对解题并没有用吗？

这里就带出一个数独中偏理论的问题，在得到或推理出某些间接线索后，如何继续往下推理？以卡点为例，我们虽然是在三宫内得到了数对8、9，但这个数对除了对三宫有占位效果外，不要忘记它们对B行和对8列、9列同样产生了影响，我们不要把观察范围局限在三宫内，而应该在更大的范围横向和纵向观察这个数对是否对其它区域产生了关键性的限制影响。

我们来观察9列，发现由于这个数对的出现，可以利用数字1对9列排除得到确定的1，见下图：

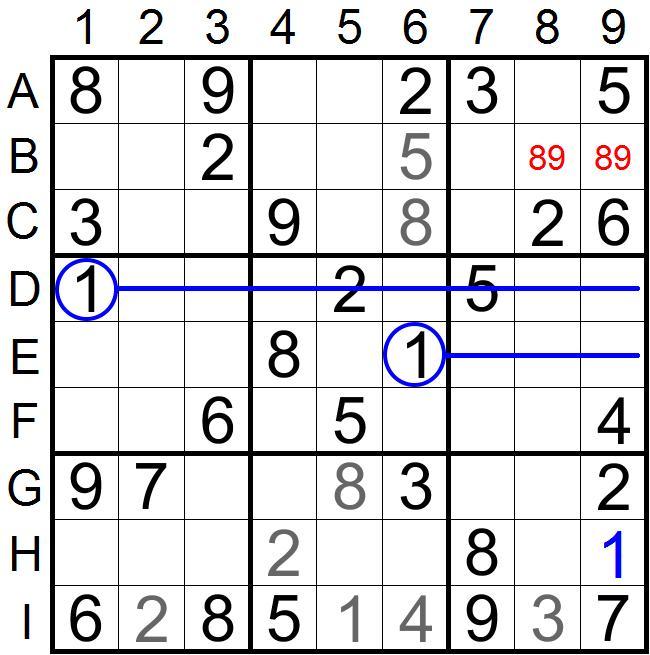
利用三宫的8、9数对占位，然后利用数字1对9列排除，得到H9格填1，这就是上期这个卡点的标准答案，不知道你是否找到了呢？我们在下面继续介绍几种数对占位的其它情况，让大家对数对占位法理解更加深入一些。

如上图所示，B行、C行和7列都有已知数5、7，它们都对三宫产生排除效果，结合这些条件可以在三宫内的B8和B9两格内形成数对5、7的占位。从这个示例可以看出，就算一个宫内已知数很少甚至没有，也不影响数对占位的出现，只要这个宫周围某两数的条件足够多就可以形成。